Introducción
“Donald en el País de las Matemágicas” (Walt Disney Productions, 1959) es un corto animado que dura 27 minutos y muestra de manera entretenida el papel que juegan las matemáticas en el mundo real. En México, dicho corto se puede encontrar en el DVD titulado “Fábulas de Disney, Volumen tres”.
El corto completo también está disponible en YouTube con doblaje en español latinoamericano. Una de las partes que más me gusta es la referente a la explicación de la sección de oro (conocida también como número áureo, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción, entre otros). Invito al lector a que vea el video; estoy seguro que le resultará muy interesante. A mi me gusta ponérselos a mis alumnos antes de introducir el tema de gráficas de tortuga.
Calculando \(\varphi\) de manera algebraica
La sección de oro, representada por la letra griega \(\varphi\) (fi), es un número irracional (esto quiere decir que no se puede escribir como una fracción). Se obtiene dividiendo una línea en dos partes, una larga y otra corta, de manera que la parte larga dividida entre la corta es igual al total de toda la línea dividido entre la parte larga. Gráficamente se puede expresar de la siguiente forma:
Toda la línea mide una unidad. Las dos partes de la línea son (x) y (1 - x), que corresponden a la parte larga y corta respectivamente. Por tanto, la sección de oro se puede expresar usando la ecuación (1): \begin{equation} \varphi = \frac{1}{x} = \frac{x}{1-x} \tag{1} \end{equation} \begin{equation} 1(1 - x) = x(x) \end{equation} \begin{equation} 1 - x = x ^ 2 \end{equation} \begin{equation} x ^ 2 + x - 1 = 0 \tag{2} \end{equation} Usando simples despejes algebraicos, la razón de la ecuación (1) se puede transformar hasta llegar a (2). Para encontrar el valor de x a partir de la ecuación cuadrática (3) se puede usar la fórmula general (4) (conocida también coloquialmente en México como “la fórmula del chicharronero”, ya que hasta el señor que vende chicharrones la conoce). \begin{equation} a x ^ 2 + b x + c = 0 \tag{3} \end{equation} \begin{equation} x = \frac{-b + \sqrt{b^2 - 4ac}}{2a} \tag{4} \end{equation} A partir de (2), tenemos que a = 1, b = 1 y c = –1. Haciendo las sustituciones correspondientes en (4), se puede determinar finalmente en (5) el valor de \(\varphi\) según su definición en (1). \begin{equation} x = \frac{-(1) + \sqrt{(1)^2 - 4(1)(-1)}}{2(1)} \end{equation} \begin{equation} x = \frac{-1 + \sqrt{1 + 4}}{2} \end{equation} \begin{equation} x = \frac{\sqrt{5}-1}{2} \end{equation} \begin{equation} \varphi = \frac{1}{x} = \frac{2}{\sqrt{5}-1} = 1.61803398874989484820\ldots \tag{5} \end{equation}
Usando números de Fibonacci para calcular \(\varphi\)
Otra forma de calcular la sección de oro es utilizando los números de Fibonacci. Se puede obtener una aproximación de \(\varphi\) al dividir fib(n) entre fib(n-1), para n > 1. Entre mayor sea el valor de n, mejor será la aproximación de \(\varphi\). Poniendo esto en código de Python para n = 100 tenemos:def fib(n): a = 1 b = 0 for i in range(n): a, b = b, a + b return b def fi(n): return fib(n) / fib(n - 1) print('\N{Mathematical Italic Small Phi} =', fi(100))NOTA: Todo el código de Python presentado en este artículo requiere Python 3.x.
La salida producida es:
𝜑 = 1.618033988749895El resultado es exactamente el esperado hasta el decimocuarto dígito después del punto decimal.
Usando \(\varphi\) para calcular los números de Fibonacci
También es posible calcular el elemento n-ésimo de la sucesión de Fibonacci utilizando la razón áurea \(\varphi\) a partir de la siguiente fórmula:\begin{equation} \textrm{fib} (n) = \frac{\varphi^n - (1 - \varphi)^n}{\sqrt{5}} \end{equation} Podemos verificar que dicha fórmula produce los valores correctos corriendo el siguiente programa:
from math import sqrt fi = 1.618033988749895 def fib(n): return (fi ** n - (1 - fi) ** n) / sqrt(5) for i in range(16): print("fib({0}) = {1}".format(i, fib(i)))Esta es la salida correspondiente:
fib(0) = 0.0 fib(1) = 1.0 fib(2) = 1.0 fib(3) = 2.0 fib(4) = 3.0000000000000004 fib(5) = 5.000000000000001 fib(6) = 8.000000000000002 fib(7) = 13.000000000000002 fib(8) = 21.000000000000004 fib(9) = 34.00000000000001 fib(10) = 55.000000000000014 fib(11) = 89.00000000000003 fib(12) = 144.00000000000006 fib(13) = 233.00000000000006 fib(14) = 377.00000000000017 fib(15) = 610.0000000000003Podemos notar algunos pequeños errores asociados a la perdida de precisión en los dígitos posteriores al punto decimal. Esto es inherente al uso de números de punto flotante. Aún así, los resultados son bastante próximos a los valores esperados.
La espiral dorada
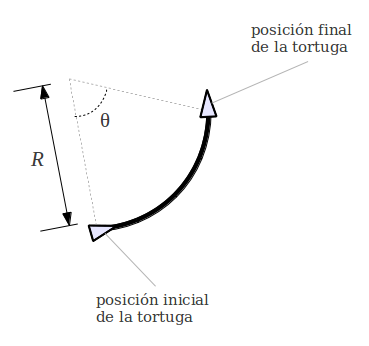
La espiral dorada (también conocida como espiral áurea) es una espiral logarítmica cuyo factor de crecimiento es \(\varphi\). Resulta relativamente sencillo dibujar dicha espiral usando Python y gráficas de tortuga. El truco consiste en saber cómo dibujar un arco. El móduloturtle de Python tiene una función llamada circle() que recibe dos argumentos (realmente son tres, pero podemos ignorar el tercer argumento): un radio R (en pixeles) y un ángulo θ (en grados). La siguiente imagen muestra la manera de interpretar los argumentos de la función circle():Si θ = 360 (o si dicho argumento se omite), entonces la función
circle() dibuja un círculo completo con radio R.La espiral dorada está conformada por n arcos dibujados de forma consecutiva, cada arco de 90° y con un radio que se multiplica por \(\varphi\) en cada iteración. En este caso, decimos que n es el orden de la espiral. El siguiente código muestra como combinar todos estos elementos:
from turtle import * # Importar las funciones de gráficas # de tortuga. fi = 1.618033988749895 # Definir 𝜑 (sección de oro). def espiral(n): radio = 10 # Definir radio inicial del primer # arco. for i in range(n): # Repetir n veces. circle(radio, 90) # Dibujar el arco de un cierto radio # y 90 grados. radio *= fi # Aumentar radio por el factor 𝜑. hideturtle() # Esconder la tortuga. color('SteelBlue') # Establecer color de la pluma: azul # metálico. pensize(20) # Establecer tamaño de la pluma: 20 pixeles. speed('fastest') # Establecer velocidad de tortuga: máxima. setheading(270) # Apuntar la tortuga hacia el sur. espiral(8) # Dibujar espiral de orden 8. done() # Evitar que la ventana se cierre # inmediatamente.Al ejecutar el programa obtenemos la siguiente figura:
 |
| Espiral dorada de orden 8. |
from turtle import * fi = 1.618033988749895 def cuadro(longitud): """Dibuja un cuadrado relleno cuyos lados son de tamaño 'longitud'. """ begin_fill() for i in range(4): fd(longitud) lt(90) end_fill() def rectangulo_dorado(n, longitud): """Dibuja un rectángulo dorado compuesto de 'n' cuadrados. El primer cuadrado tiene sus lados de tamaño 'longitud'. """ for i in range(n): cuadro(longitud) # Mover la tortuga a la esquina contraria y girarla # 90 grados a la izquierda. fd(longitud) lt(90) fd(longitud) longitud *= fi def espiral_dorada(n, radio): """Dibuja una espiral dorada compuesta de 'n' arcos. El primer arco tiene un radio de tamaño 'radio'. """ for i in range(n): circle(radio, 90) radio *= fi def espiral(n, radio): """Dibuja una espiral dorada de orden 'n' sobre el rectángulo dorado que lo alberga. El primer arco/cuadro tiene un radio/lado de tamaño 'radio'. """ color('White') fillcolor('SteelBlue') pensize(1) rectangulo_dorado(n, radio) # Regresa la tortuga al centro de la pantalla pero sin # dibujar por su paso. penup() home() pendown() color('Gold') pensize(4) espiral_dorada(n, radio) hideturtle() speed('slow') espiral(11, 2) done()El código anterior es más elaborado pero el resultado bien vale la pena:
 |
| Espiral dorada de orden 11 sobre su rectángulo dorado correspondiente. |


¡Qué interesante! La duda es nada más cómo se dedujo la fórmula para sacar aproximaciones de los números de Fibonacci utilizando la razón áurea φ. No me pierdo EduPython aunque mi trabajo no tiene que ver con programación. Es bueno recordar. Saludos maestro.
ResponderBorrarAbraham de Moivre dio a conocer esta fórmula en 1718, aunque se le conoce como "fórmula de Binet" ya que fue descrita por Jacques Philippe Marie Binet en 1843.
BorrarDesconozco cómo fue que se dedujo, pero la demostración puede ser consultada en muchos sitios en Internet. Por ejemplo:
http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibformproof.html
También es interesante que la fórmula para fi expresada en (5) puede multiplicarse en el denominador y númerador por sqrt(5)+1 y después de simplificar queda
ResponderBorrarfi = (sqrt(5)+1)/2
Una expresión que puede representarse geométricamente usando regla y compás ;)
Interesante observación. Gracias José Manuel.
Borrar