Introducción
Para mucha gente (yo incluido), la idea de tener que documentar un programa genera el mismo entusiasmo que cuando pensamos sobre la ingesta diaria recomendada de verduras. Son de esas cosas que sabemos que son buenas y debemos procurar, pero definitivamente no nos fascinan.Sin embargo, la verdad es ésta: no importa lo fabuloso que sea un programa, nadie lo usará si no queda claro la manera de utilizarlo. En este sentido la documentación juega un rol primordial. Aunque yo sea el único usuario de mi programa, resulta más sencillo entender y reutilizar lo que escribí hace seis meses si cuento con una documentación adecuada.
Nos debe quedar claro que, como maestros de programación, tenemos la responsabilidad de inculcar la importancia de la documentación a nuestros alumnos.
Pero, ¿por qué nos disgusta tanto la tarea de escribir documentación para nuestros programas? La razón es simple: es más divertido escribir código que documentarlo. Empero, si deseamos que nuestros programas trasciendan más allá del momento en que los escribimos necesitamos dedicarles algo de tiempo para documentarlos.
Una buena noticia es que Python cuenta con un mecanismo bastante sencillo y conveniente para elaborar la documentación técnica de un programa. A continuación expondré dicho mecanismo.
Cadenas de documentación
En Python, un docstring o cadena de documentación es una literal de cadena de caracteres que se coloca como primer enunciado de un módulo, clase, método o función, y cuyo propósito es explicar su intención. Un ejemplo sencillo (todos estos ejemplos funcionan en Python 3):def promedio(a, b): 'Calcula el promedio de dos números.' return (a + b) / 2Un ejemplo más completo:
def formula_cuadratica(a, b, c): """Resuelve una ecuación cuadrática. Devuelve en una tupla las dos raíces que resuelven la ecuación cuadrática: ax^2 + bx + c = 0. Utiliza la fórmula general (también conocida coloquialmente como el "chicharronero"). Parámetros: a -- coeficiente cuadrático (debe ser distinto de 0) b -- coeficiente lineal c -- término independiente Excepciones: ValueError -- Si (a == 0) """ if a == 0: raise ValueError( 'Coeficiente cuadrático no debe ser 0.') from cmath import sqrt discriminante = b ** 2 - 4 * a * c x1 = (-b + sqrt(discriminante)) / (2 * a) x2 = (-b - sqrt(discriminante)) / (2 * a) return (x1, x2)La cadena de documentación en el segundo ejemplo es una cadena multi-líneas, la cual comienza y termina con triples comillas (
"""). Aquí se pueden observar el uso de las convenciones establecidas en el PEP 257 (Python Enhancement Proposals):- La primera línea de la cadena de documentación debe ser una línea de resumen terminada con un punto. Debe ser una breve descripción de la función que indica los efectos de ésta como comando. La línea de resumen puede ser utilizada por herramientas automáticas de indexación; es importante que quepa en una sola línea y que esté separada del resto del docstring por una línea en blanco.
- El resto de la cadena de documentación debe describir el comportamiento de la función, los valores que devuelve, las excepciones que arroja y cualquier otro detalle que consideremos relevante.
- Se recomienda dejar una línea en blanco antes de las triples comillas que cierran la cadena de documentación.
__doc__ el cual contiene su respectivo comentario de documentación. A partir de los ejemplos anteriores podemos inspeccionar la documentación de las funciones promedio y formula_cuadratica desde el shell de Python:
>>> promedio.__doc__ 'Calcula el promedio de dos números.' >>> formula_cuadratica.__doc__ 'Resuelve una ecuación cuadrática.\n\n Devuelve en una tupla las dos raíces que resuelven la\n ecuación cuadrática:\n \n ax^2 + bx + c = 0.\n\n Utiliza la fórmula general (también conocida\n coloquialmente como el "chicharronero").\n\n Parámetros:\n a -- coeficiente cuadrático (debe ser distinto de 0)\n b -- coeficiente lineal\n c -- término independiente\n\n Excepciones:\n ValueError -- Si (a == 0)\n \n 'Sin embargo, si se está usando el shell de Python es mejor usar la función
help(), dado que la salida producida queda formateada de manera más clara y conveniente:>>> help(promedio)
Help on function promedio in module __main__:
promedio(a, b)
Calcula el promedio de dos números.
>>> help(formula_cuadratica)
Help on function formula_cuadratica in module __main__:
formula_cuadratica(a, b, c)
Resuelve una ecuación cuadrática.
Devuelve en una tupla las dos raíces que resuelven la
ecuación cuadrática:
ax^2 + bx + c = 0.
Utiliza la fórmula general (también conocida
coloquialmente como el "chicharronero").
Parámetros:
a -- coeficiente cuadrático (debe ser distinto de 0)
b -- coeficiente lineal
c -- término independiente
Excepciones:
ValueError -- Si (a == 0)
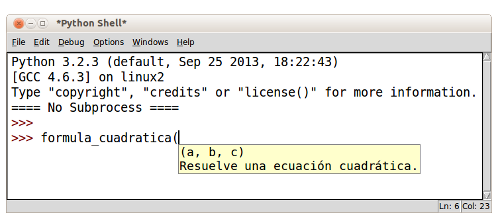
Ciertas herramientas, por ejemplo shells o editores de código, pueden ayudar a visualizar de manera automática la información contenida en los comentarios de documentación. La siguiente imagen muestra como el shell del ambiente de desarrollo integrado IDLE muestra la línea de resumen como descripción emergente (tool tip) al momento en que un usuario teclea el nombre de la función:Generando documentación en páginas de HTML
Los docstrings se pueden usar también para producir documentación en páginas de HTML que pueden ser consultadas usando un navegador de web. Para ello se usa el comandopydoc desde una terminal. Por ejemplo, si las dos funciones anteriores (promedio y formula_cuadratica) se encuentran en un archivo fuente llamado ejemplos.py, podemos ejecutar el siguiente comando en una terminal dentro del mismo directorio donde está el archivo fuente:
pydoc -w ejemplosLa salida queda en el archivo
ejemplos.html, y así se visualiza desde un navegador:La documentación de pydoc explica otras monerías que puede hacer esta utilería de Python.
Docstrings vs. comentarios
Un comentario en Python inicia con el símbolo de número (#) y se extiende hasta el final de la línea. En principio los docstrings pudieran parecer similares a los comentarios, pero hay una diferencia pragmática importante: los comentarios son ignorados por el ambiente de ejecución de Python y por herramientas como pydoc; esto no es así en el caso de los docstrings. A un nivel más fundamental hay otra diferencia aún más grande entre los docstrings y los comentarios, y ésta tiene que ver con la intención:
- Los docstrings son documentación, y sirven para entender qué hace el código.
- Los comentarios sirven para explicar cómo lo hace.